AVL and B-tree Summary

AVL Tree

An AVL tree is a subtype of binary search tree. Named after it's inventors Adelson, Velskii and Landis, AVL trees have the property of dynamic self-balancing in addition to all the properties exhibited by binary search trees.

A BST is a data structure composed of nodes. It has the following guarantees:

1. Each tree has a root node (at the top).
2. The root node has zero, one or two child nodes.
3. Each child node has zero, one or two child nodes, and so on.
4. Each node has up to two children.
5. For each node, its left descendants are less than the current node, which is less than the right descendants.
6. The difference between the depth of right and left subtrees cannot be more than one. In order to maintain this guarantee, an implementation of an AVL will include an algorithm to re-balance the tree when adding an additional element would upset this guarantee.

Right Rotation and Left Rotation

AVL Insertion Process

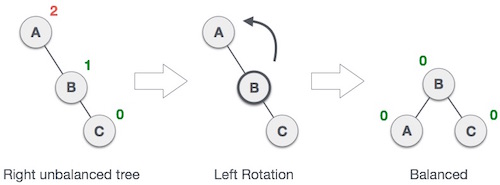
• If there is an imbalance in left child of right subtree, then you perform a left-right rotation.

• If there is an imbalance in left child of left subtree, then you perform a right rotation.

• If there is an imbalance in right child of right subtree, then you perform a left rotation.

• If there is an imbalance in right child of left subtree, then you perform a right-left rotation.

AVL Tree Rotations Types:
Single Left Rotation (LL Rotation)
Single Right Rotation (RR Rotation)
Left Right Rotation (LR Rotation)
Right Left Rotation (RL Rotation)
Time Analysis Of AVL Trees

Application of AVL Trees

1. Every node has at most m children.
2. Every non-leaf node (except root) has at least ⌈m/2⌉ child nodes.
3. The root has at least two children if it is not a leaf node.
4. A non-leaf node with k children contains k − 1 keys.
5. All leaves appear in the same level and carry no information.

Internal nodes
Internal nodes are all nodes except for leaf nodes and the root node. They are usually represented as an ordered set of elements and child pointers. Every internal node contains a maximum of U children and a minimum of L children. Thus, the number of elements is always 1 less than the number of child pointers (the number of elements is between L−1 and U−1). U must be either 2L or 2L−1; therefore each internal node is at least half full. The relationship between U and L implies that two half-full nodes can be joined to make a legal node, and one full node can be split into two legal nodes (if there’s room to push one element up into the parent). These properties make it possible to delete and insert new values into a B-tree and adjust the tree to preserve the B-tree properties.

The root node
The root node’s number of children has the same upper limit as internal nodes, but has no lower limit. For example, when there are fewer than L−1 elements in the entire tree, the root will be the only node in the tree with no children at all.

Leaf nodes
In Knuth's terminology, leaf nodes do not carry any information. The internal nodes that are one level above the leaves are what would be called "leaves" by other authors: these nodes only store keys (at most m-1, and at least m/2-1 if they are not the root) and pointers to nodes carrying no information.

AVL trees have an additional guarantee:

AVL trees have a worst case lookup, insert and delete time of O(log n).

An insertion similar to a normal Binary Search Tree insertion. After inserting, you fix the AVL property using left or right rotations.

An AVL tree is a self-balancing binary search tree. An AVL tree is a binary search tree which has the following properties: The sub-trees of every node differ in height by at most one, and every sub-tree is an AVL tree.

AVL tree checks the height of the left and the right sub-trees and assures that the difference is not more than 1. This difference is called the Balance Factor. The height of an AVL tree is always O(Logn) where n is the number of nodes in the tree.

In AVL tree, after performing every operation like insertion and deletion we need to check the balance factor of every node in the tree. If every node satisfies the balance factor condition then we conclude the operation otherwise we must make it balanced. We use rotation operations to make the tree balanced whenever the tree is becoming imbalanced due to any operation.

Rotation operations are used to make a tree balanced.There are four rotations and they are classified into two types:

In LL Rotation every node moves one position to left from the current position.

In RR Rotation every node moves one position to right from the current position.

The LR Rotation is combination of single left rotation followed by single right rotation. In LR Rotation, first every node moves one position to left then one position to right from the current position.

The RL Rotation is combination of single right rotation followed by single left rotation. In RL Rotation, first every node moves one position to right then one position to left from the current position.

AVL tree is binary search tree with additional property that difference between height of left sub-tree and right sub-tree of any node can’t be more than 1.

Algorithm Average Worst case: Space: o(n), Time: o(n).

AVL trees are beneficial in the cases where you are designing some database where insertions and deletions are not that frequent but you have to frequently look-up for the items present in there.

B-Tree

B-tree is a self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree generalizes the binary search tree, allowing for nodes with more than two children.Unlike other self balancing binary search trees, the B-tree is well suited for storage systems that read and write relatively large blocks of data, such as discs. It is commonly used in databases and file systems.

According to Knuth's definition, a B-tree of order m is a tree which satisfies the following properties:

Each internal node's keys act as separation values which divide its subtrees. For example, if an internal node has 3 child nodes (or subtrees) then it must have 2 keys: a₁ and a₂. All values in the leftmost subtree will be less than a₁, all values in the middle subtree will be between a₁ and a₂, and all values in the rightmost subtree will be greater than a₂.

A B-tree of depth n+1 can hold about U times as many items as a B-tree of depth n, but the cost of search, insert, and delete operations grows with the depth of the tree. As with any balanced tree, the cost grows much more slowly than the number of elements.

Some balanced trees store values only at leaf nodes, and use different kinds of nodes for leaf nodes and internal nodes. B-trees keep values in every node in the tree except leaf nodes.

Informal Description

In B-trees, internal nodes can have a variable number of child nodes within some pre-defined range. When data is inserted or removed from a node, its number of child nodes changes. In order to maintain the pre-defined range, internal nodes may be joined or split. Because a range of child nodes is permitted, B-trees do not need re-balancing as frequently as other self-balancing search trees, but may waste some space, since nodes are not entirely full. The lower and upper bounds on the number of child nodes are typically fixed for a particular implementation. For example, in a 2-3 B-tree (often simply referred to as a 2-3 tree), each internal node may have only 2 or 3 child nodes.

Each internal node of a B-tree contains a number of keys. The keys act as separation values which divide its subtree. For example, if an internal node has 3 child nodes (or subtrees) then it must have 2 keys: a₁ and a₂. All values in the leftmost subtree will be less than a₁, all values in the middle subtree will be between a₁ and a₂, and all values in the rightmost subtree will be greater than a₂.

Usually, the number of keys is chosen to vary between d and 2d, where d is the minimum number of keys, and d + 1 is the minimum degree or branching factor of the tree. In practice, the keys take up the most space in a node. The factor of 2 will guarantee that nodes can be split or combined. If an internal node has 2d keys, then adding a key to that node can be accomplished by splitting the hypothetical 2d + 1 key node into two d key nodes and moving the key that would have been in the middle to the parent node. Each split node has the required minimum number of keys. Similarly, if an internal node and its neighbor each have d keys, then a key may be deleted from the internal node by combining it with its neighbor. Deleting the key would make the internal node have d - 1 keys; joining the neighbor would add d keys plus one more key brought down from the neighbor's parent. The result is an entirely full node of 2d keys.

The number of branches (or child nodes) from a node will be one more than the number of keys stored in the node. In a 2-3 B-tree, the internal nodes will store either one key (with two child nodes) or two keys (with three child nodes). A B-tree is sometimes described with the parameters (d + 1) - (2d + 1) or simply with the highest branching order, (2d + 1).

A B-tree is kept balanced after insertion by splitting a would-be overfilled node, of 2d + 1 keys, into two d-key siblings and inserting the mid-value key into the parent. Depth only increases when the root is split, maintaining balance. Similarly, a B-tree is kept balanced after deletion by merging or redistributing keys among siblings to maintain the d-key minimum for non-root nodes. A merger reduces the number of keys in the parent potentially forcing it to merge or redistribute keys with its siblings, and so on. The only change in depth occurs when the root has two children, of d and (transitionally) d - 1 keys, in which case the two siblings and parent are merged, reducing the depth by one.

This depth will increase slowly as elements are added to the tree, but an increase in the overall depth is infrequent, and results in all leaf nodes being one more node farther away from the root.

B-trees have substantial advantages over alternative implementations when the time to access the data of a node greatly exceeds the time spent processing that data, because then the cost of accessing the node may be amortized over multiple operations within the node. This usually occurs when the node data are in secondary storage such as disk drives. By maximizing the number of keys within each internal node, the height of the tree decreases and the number of expensive node accesses is reduced. In addition, re-balancing of the tree occurs less often. The maximum number of child nodes depends on the information that must be stored for each child node and the size of a full disk block or an analogous size in secondary storage. While 2-3 B-trees are easier to explain, practical B-trees using secondary storage need a large number of child nodes to improve performance.

Example AVL and B-trees:
Insert: 5, 6, 7, 0, 4, 3, 8
Delete: 3, 4, 8

AVL Tree:


B-tree: